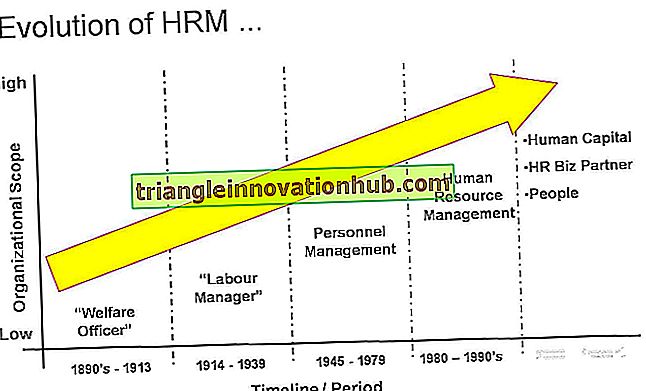
Methoden voor probleemoplossing in twee fasen in lineaire programmering: eerste en tweede fase

In deze methode is het probleem opgelost in twee fasen zoals hieronder weergegeven.

Eerste fase:

(a) Alle voorwaarden op RHS moeten niet-negatief zijn. Als sommige -ve zijn, dan moeten ze gemaakt + zijn zoals eerder uitgelegd.

(b) Expressbeperkingen in standaardvorm.

(d) Vorm een nieuwe doelfunctie W die bestond uit de som van alle kunstmatige variabelen

W = A ₁ + A ₂ + ........................ + A _m

Functie (W) staat bekend als onuitvoerbaarheidsvorm.

(e) Functie W moet tot een minimum worden beperkt, afhankelijk van de beperkingen van het oorspronkelijke probleem en de optimale basisaanvaardbare oplossing wordt verkregen.

Een van de volgende drie gevallen kan zich voordoen:

(ik doe mee. W> 0 en ten minste één kunstmatige variabele verschijnt in kolom "Basisvariabelen" op positief niveau. In dergelijke gevallen bestaat er geen haalbare oplossing voor de originele LPP en wordt de procedure gestopt.

(ii) Min. W = 0 en ten minste één kunstmatige variabele verschijnt in kolom "Basisvariabelen" op nulniveau. In een dergelijk geval kan de optimale basisuitvoerbare oplossing voor het onuitvoerbaarheidsformulier al dan niet een basisuitvoerbare oplossing zijn voor de gegeven (oorspronkelijke) LPP. Om een basisuitvoerbare oplossing te verkrijgen, gaan we door fase I en proberen alle kunstmatige variabelen uit te drijven basis en ga vervolgens naar fase II.

(iii) Min. W = 0 en geen kunstmatige variabele verschijnt in de kolom "Huidige variabelen" huidige oplossing. In een dergelijk geval is een eenvoudige, haalbare oplossing voor de oorspronkelijke LPP gevonden. Ga door naar fase II.

Tweede fase:

Gebruik de optimale basis haalbare oplossing van fase I als een startoplossing voor de originele LPP. Gebruik de simplex methode om iteraties tot een optimale basis haalbare oplossing te maken, want deze wordt verkregen.

Opgemerkt kan worden dat de nieuwe doelfunctie W altijd van het minimaliseringstype is, ongeacht of de gegeven (oorspronkelijke) LPP van maximalisatie- of minimaliseringstype is. Laten we het volgende voorbeeld nemen.

Voorbeeld 1 (tweefasige simplexmethode):

Gebruik tweefasige simplex-methode om

Minimaliseren Z = -3X - 2Y - 2Z

Onderworpen aan 5X + 7Y + 4Z <7

-4X + 7Y + 5Z> -2

3X + 4 V - 6Z> 29/7

X, Y, Z> 0

Oplossing:

Eerste fase

Het bestaat uit de volgende stappen.

(a) In de tweede beperking is RHS -ve, daarom is het + ve gemaakt door vermenigvuldigen met minteken aan beide zijden

4X - 7Y - 5Z <2

(b) Slack-variabelen toevoegen aan de beperkingen

5X + 7Y + 4Z + S ₁ = 7

4X - 7Y - 5Z + S ₂ = 2

3X + 4Y - 6Z - S ₃ = 29/7

waar X, Y, Z, S ₁, S ₂, S ₃ > 0

(c) Zet X = Y = Z = 0, we krijgen S ₁ = 7, S ₂ = 2, S ₃ = -29/7. als eerste oplossing. Maar serie S ₃ is -ve, we zullen kunstmatige variabele A, dat wil zeggen toevoegen

3X + 4Y- 6Z- S ₃ + A ₁ = 29/7

(d) Objectieve functie die het minimaliseringstype is, is het maximalisatietype, dwz

Maximaliseer Z = 3X + 2Y + 2Z

(e) We introduceren nieuwe objectieve functie W = A1 voor de eerste fase die moet worden geminimaliseerd.

(f) Substitutie van X = Y = Z = S ₃ = 0 in de beperkingen die we krijgen S ₁ = 7, S ₂ = 2, / Al = 29/7 als aanvankelijke basis haalbare oplossing Tabel 1 indien gevormd.

Voorgevormde optimalisatietest

Aangezien Cj-Ej onder dezelfde kolommen negatief is (minimalisatieprobleem), kan de huidige, voor de basis haalbare oplossing worden verbeterd.

Itereren naar en optimale oplossing:

Herhalingen uitvoeren om een optimale oplossing te krijgen.

Vervang S ₁ door X ₂ . dit wordt getoond in de onderstaande tabel

In tabel is er een gelijkspel voor de sleutelrij X kolom is de sleutel kolom en y kolom is de eerste kolom van de identiteit. Na de methode voor het binden van het stropdas vinden we dat de kolom de das niet verbreekt. De volgende kolom van de identiteit, dwz S ₂ -kolom, geeft A _1- worp als de sleutelrij. Dus (1/7) is het belangrijkste element eenheid in tafel

Vervang A ₁ door X zoals weergegeven in onderstaande tabel

Tabel 5 geeft de optimale oplossing. Ook sinds minimum W = 0 en er is geen kunstmatige variabele in de basisvariabelen dat wil zeggen in de huidige oplossing, geeft tabel 5 basis haalbare oplossing voor de fase-II

Tweede fase:

De oorspronkelijke doelfunctie is

Maximaliseer Z = 3x + 2y + 2Z + OS, + 0S ₂ + 0S ₃

Het moet gemaximaliseerd worden met behulp van originele beperkingen. Met behulp van de oplossing van fase I als de startoplossing voor fase II en het uitvoeren van de berekening met behulp van simplex-algoritme, krijgen we tabel 6